Diffie-Hellman Key Exchange: A Secure Handshake in the Digital World

13 Jul 2025

The Diffie-Hellman (DH) key exchange is a foundational mathematical method that enables two parties to securely establish a shared secret key over an insecure public channel, even if they have no prior knowledge of each other. This secret key is crucial for subsequent secure communication using symmetric-key encryption. The protocol’s security relies on the concept of a one-way function, making it easy to compute in one direction but extremely difficult to reverse.

The Lock and Key Analogy

To understand how Diffie-Hellman works, consider an analogy involving padlocks and keys:

1. Alice’s Action: Alice places a secret message or item inside a box and locks it with a padlock that only she has the key for.

2. Alice to Bob: She sends this double-locked box to Bob over the insecure channel.

3. Bob’s Action: Bob receives the box and adds his own padlock to it, which only he has the key for.

4. Bob to Alice: Bob sends the box back to Alice.

5. Alice Unlocks: Alice receives the box and removes her padlock using her key.

6. Alice to Bob (Again): Alice sends the box back to Bob.

7. Bob Unlocks: Bob removes his padlock using his key, opening the box and gaining access to the secret message.

Both Alice and Bob have successfully exchanged the secret without sending their keys over the insecure channel. An eavesdropper observing the process would only see the box being exchanged with different locks on it, but would not be able to open the box without both keys.

The Mathematical Foundation and Example

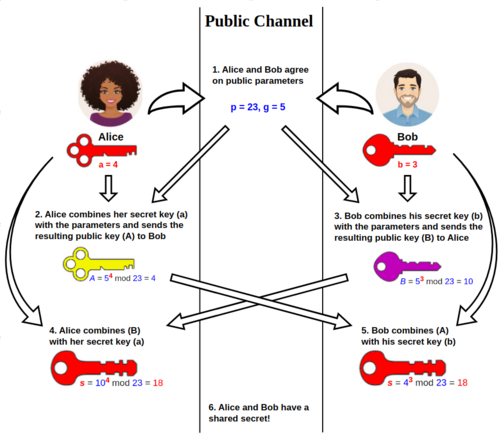
In the real-world Diffie-Hellman exchange, the process is implemented using large numbers and modular exponentiation. The security relies on the difficulty of solving the discrete logarithm problem.

Here is a simple example computation of the Diffie-Hellman key exchange:

Publicly Agreed Values:

• Modulus p = 23

• Base g = 5

The Exchange:

1. Alice’s Secret and Public Key:

   • Alice chooses a secret integer a = 4.

   • She computes her public value A = 5^4 mod 23 = 4.

   • Alice sends A = 4 to Bob.

2. Bob’s Secret and Public Key:

   • Bob chooses a secret integer b = 3.

   • He computes his public value B = 5^3 mod 23 = 10.

   • Bob sends B = 10 to Alice.

Shared Secret Calculation:

1. Alice’s Calculation: Alice computes the shared secret s using Bob’s public value B and her secret a:

   • s = B^a mod p = 10^4 mod 23 = 18

2. Bob’s Calculation: Bob computes the shared secret s using Alice’s public value A and his secret b:

   • s = A^b mod p = 4^3 mod 23 = 18

Both Alice and Bob arrive at the same shared secret, 18. This shared secret can now be used for secure communication.

Reference

• Diffie–Hellman key exchange (Wikipedia)